Mapas de karnaugh

Un mapa de Karnaugh también conocido como tabla de Karnaugh o diagrama de Veitch es un diagrama para la simplificación de circuitos lógicos. Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más económica posible se utiliza este método.

El mapa de Karnaugh consiste en una representación bidimensional de la función que se quiere simplificar. Si la función viene expresada como una tabla de verdad, entonces el mapa de Karnaugh puede verse como una forma alternativa de representación 2D. Puesto que la tabla de verdad de una función de n variables posee 2n filas, el mapa de Karnaugh correspondiente debe poseer también 2n celdas. La construcción de la tabla de Karnaugh pasa por codificar cada celda en código binario reflejado (o código Gray) de manera que celdas adyacentes tengan un código que difiere en un solo dígito.

Ejemplo: Se tiene la siguiente tabla de verdad para tres variables. Se desarrolla la función lógica basada en ella. (primera forma canónica).

Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a “1”. Si A en la tabla de verdad es “0” se pone A, si B = “1” se pone B, Si C = “0” se pone C, etc.

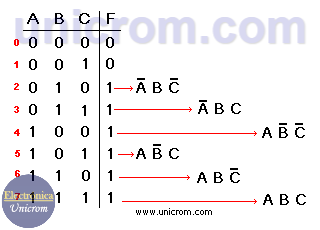
F = A B C + A B C + A B C + A B C + A B C + A B C

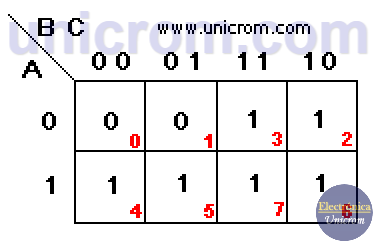
Una vez obtenida la función lógica, se implementa el mapa de Karnaugh. Este tiene 8 casillas que corresponden a 2n, donde n = 3 (número de variables (A, B, C)). 

La primera fila corresponde a A = 0 La segunda fila corresponde a A = 1 La primera columna corresponde a BC = 00 (B=0 y C=0).

La segunda columna corresponde a BC = 01 (B=0 y C=1) La tercera columna corresponde a BC = 11 (B=1 y C=1) La cuarta columna corresponde a BC = 10 (B=1 y C=0)

En el mapa de Karnaugh se han puesto “1” en las casillas que corresponden a los valores de F = “1” en la tabla de verdad. Tomar en cuenta la numeración de las filas de la tabla de verdad y la numeración de las casillas en el mapa de Karnaugh.

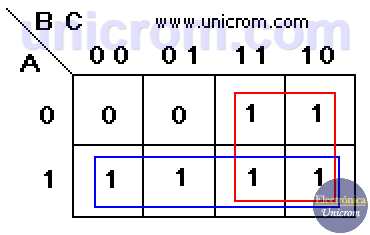
Para proceder con la simplificación, se crean grupos de “1”s que tengan 1, 2, 4, 8, 16, etc. (solo potencias de 2). Los “1”s deben estar adyacentes (no en diagonal) y mientras más “1”s tenga el grupo, mejor.

La función mejor simplificada es aquella que tiene el menor número de grupos con el mayor número de “1” s en cada grupo

Se ve del gráfico que hay dos grupos cada uno de cuatro “1”s (se permite compartir casillas entre los grupos). La nueva expresión de la función booleana simplificada se deduce del mapa de Karnaugh.

Para el primer grupo (rojo): la simplificación da B (los “1”s de la tercera y cuarta columna corresponden a B sin negar)

Para el segundo grupo (azul): la simplificación da A (los “1”s están en la fila inferior que corresponde a A sin negar).

Tabla de verdad para ejemplo de simplificación por mapa de Karnaugh

Entonces el resultado es F = B + A  ó   F = A + B

Ejemplo: Una tabla de verdad como la de la derecha da la siguiente función booleana: F = A B C + A B C + A B C + A B C

Se ve claramente que la función es un reflejo del contenido de la tabla de verdad cuando F = “1”, Con esta ecuación se crea el mapa de Karnaugh y se escogen los grupos.

Se lograron hacer 3 grupos de dos “1”s cada uno. Se puede ver que no es posible hacer grupos de 3, porque 3 no es potencia de 2. Se observa que hay una casilla que es compartida por los tres grupos.

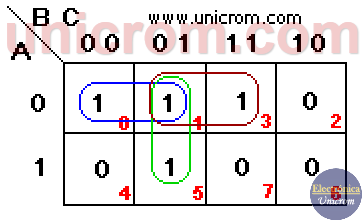
La función simplificada es: F = A B+ A C + B C. Grupo en azul: A B, grupo marrón: A C, grupo verde:B C

Reglas de simplificación

1.  Las agrupaciones son exclusivamente de unos. Esto implica que ningún grupo puede contener ningún cero.

2. Las agrupaciones únicamente pueden hacerse en horizontal y vertical. Esto implica que las diagonales están prohibidas.

3.  Los grupos han de contener 2n elementos. Es decir que cada grupo tendrá 1,2,4,8... número de unos.

4.  Cada grupo ha de ser tan grande como sea posible. Tal y como lo ilustramos en el ejemplo.

5.  Todos los unos tienen que pertenecer como mínimo a  un grupo. Aunque pueden pertenecer a más de uno.

6.  Pueden existir solapamiento de grupos.

7.  La formación de grupos también se puede producir con las celdas extremas de la tabla. De tal forma que la parte inferior se podría agrupar con la superior y la izquierda con la derecha tal y como se explica en el ejemplo.

8.  Tiene que resultar el menor número de grupos posibles siempre y cuando no contradiga ninguna de las reglas anteriores. Esto es el número de grupos ha de ser mínima.

Referencias:

Burghardt Jochen (s.f). Introducción a la Automatización Industrial "Mapa de Karnaugh". [Online]. Available: https://bookdown.org/alberto_brunete/intro_automatica/mapa-de-karnaugh.html

Electrónica Unicrom (2021). Mapas de Karnaugh – Simplificación de funciones booleanas. [Online]. Available: https://unicrom.com/mapas-de-karnaugh-simplificacion-de-funciones/

ALL ABOUT CIRCUITS (s.f). Karnaugh Maps, Truth Tables, and Boolean Expressions [Online]. Available: https://www.allaboutcircuits.com/textbook/digital/chpt-8/karnaugh-maps-truth-tables-boolean-expressions/